APPENDIX A
a) electrical - gravitational interactions;
b) magnetic - gravitational interactions

a) Calculation of electrical-gravitational interactions ratio

  
   
Take a general form of a formula, that is  
let's put that  
and to find the differential we put that  
then  we have  
 
 
 
Let's give the quantity unitary value of n and get infinitesimal variation of F  
where  n= 1 and      
With a Pindaro's jump (or flight) we can then compare gravitational forces to electrostatic ones, by the ratio of the gravitational constant (Cavendish) and  the electric constant (Coulomb)  
 
we can find the order of greatness of the proportionality constant that could give the relationship of gravity and electric forces, that is can tell us if electric force alone can interact significantly with gravity

  
)  
Is the Gravity constant (Cavendish) Is the vacuum electric constant (Coulomb)  
their ratio value is  
 
tha gives  
 


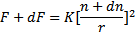
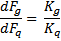
CONCLUSION : the electric fields should be enormously great to interfere with gravity, then it cannot be used to create gravity waves. The mass should also be enormously great to cause a gravitational deviation of an electric field, such the mass of our sun of also of our planet do.. The sun gravity could interfere with an electric field, because the sun mass value is greatest

 

 
  

a) Calculation of magnetic - gravitational interactions ratio

  
        If you use the Gilbert hypothesis, the formula assumes the same general shape that is  


 
where 

 

  
We can then roughly compare the gravity forces to the magnetic ones, calulating the ratio between gravitational and magnetic constants  
 

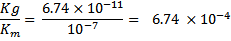
CONCLUSION : using magnetic materials with very high permeability one can estimate roughly that might be able to produce very strong magnetic fields , which may weakly interfere with the gravitational field.